Проектирование баз данных: иерархические структуры. Деревья в SQL
Материал этой статьи послужил основой для одной из глав книги "СУБД для программиста. Базы данных изнутри". Вариант статьи для научного издания опубликован в журнале "Информационно-управляющие системы" №6 2013, он содержит больше теоретических сведений и формул. Статья также опубликована в журнале "Мир ПК" №3 2007 г.
Содержание
Введение
Примеры древовидных структур могут быть найдены в разных предметных областях: классификация товаров, контрагентов, комплектация изделия, иерархия должностей, административно-территориальное деление, генеалогическое древо, наконец, просто дерево перебора вариантов или дерево классов.
В общем случае все сводится к моделированию многоуровневой связи «главный—подчиненный», «предок—потомок», «общий—конкретный». Говоря более строгим математическим языком, мы моделируем граф без циклов.
Не углубляясь в теорию графов, в рамках статьи мы рассмотрим наиболее часто встречающиеся варианты реализации древовидных структур в базах данных. В качестве примера используется Microsoft SQL Server 2005 и выше (любая редакция), но, познакомившись с общими принципами, вы сможете без затруднений перенести реализацию на любую другую СУБД.
Список смежности
Это интуитивно понятный способ организации дерева: замыкаем связь таблицы на саму себя (рефлексивная связь), рис. 1.
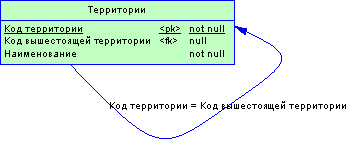
Рис.1. Реализация на основе матрицы смежности
Как известно из теории, граф можно представить в виде матрицы смежности, где на пересечении i-ой строки и j-го столбца стоит "1", если между узлами (вершинами) графа, с номерами i и j, соответственно, есть связь (ребро, дуга), или "0" в противном случае. Матрица может быть представлена в виде списка (множества) пар с номерами (идентификаторами, кодами) вершин по принципу: есть пара - есть дуга, нет пары - нет связи.
Моделирование корневых вершин осуществляется внесением записей с пустой (NULL) ссылкой на предка (в данном случае, "Код вышестоящей территории"). Для выполнения часто используемых выборок требуется поддержка рекурсивных запросов. Если СУБД не поддерживает такие запросы, то выборки придется строить с использованием механизмов временных таблиц и хранимых процедур (функций). Рассмотрим примеры запросов.
Выборка поддерева по заданному узлу (здесь и далее по тексту используем синтаксис MS SQL Server 2005):
WITH Поддерево ("Код территории", "Код вышестоящей территории", Наименование, Уровень)
AS (
SELECT "Код территории", "Код вышестоящей территории", Наименование, 1
FROM Территории
WHERE "Код вышестоящей территории" = 40288000 -- корень поддерева или IS NULL для корня целого дерева
UNION ALL
SELECT Территории."Код территории", Территории."Код вышестоящей территории", Территории.Наименование, Уровень + 1
FROM Территории
INNER JOIN Поддерево ON Территории."Код вышестоящей территории" = Поддерево."Код территории"
WHERE Территории."Код вышестоящей территории" IS NOT NULL
)
SELECT "Код территории", "Код вышестоящей территории", Наименование, Уровень
FROM Поддерево
Выборка всех предков (путь к узлу от корня):
WITH Поддерево ("Код территории", "Код вышестоящей территории", Наименование, Уровень)
AS (
SELECT "Код территории", "Код вышестоящей территории", Наименование, 1
FROM Территории
WHERE "Код территории" = 40288000 -- узел
UNION ALL
SELECT Территории."Код территории", Территории."Код вышестоящей территории", Территории.Наименование, Уровень + 1
FROM Территории
INNER JOIN Поддерево ON Территории."Код территории" = Поддерево."Код вышестоящей территории"
)
SELECT "Код территории", "Код вышестоящей территории", Наименование, (
SELECT MAX(Уровень)
FROM Поддерево
) - Уровень
FROM Поддерево
Проверка, входит ли узел в поддерево, определяемое своим корнем (например, входит ли данный товар в группу одного из верхних уровней, "Кисточка" в "Инструменты для ремонта"):
WITH Поддерево ("Код территории", "Код вышестоящей территории", Наименование, Уровень)
AS (
SELECT "Код территории", "Код вышестоящей территории", Наименование, 1
FROM Территории
WHERE "Код территории" = 40288000 -- узел, проверяемый на вхождение
UNION ALL
SELECT Территории."Код территории", Территории."Код вышестоящей территории", Территории.Наименование, Уровень + 1
FROM Территории
INNER JOIN Поддерево ON Территории."Код территории" = Поддерево."Код вышестоящей территории"
)
SELECT result = CASE
WHEN EXISTS (
SELECT 1
FROM Поддерево
WHERE "Код территории" = 40260000 /* корень поддерева */
)
THEN 'Узел входит в поддерево'
ELSE 'Узел НЕ входит в поддерево'
END
Преимущества и недостатки
| Простота структуры (таблиц/ссылок/минимальное количество полей) | 1/1/3 |
|---|---|
| Прямая выборка всех детей узла | да |
| Прямая выборка поддерева (всех потомков узла) | нет, рекурсия |
| Прямая выборка пути от узла до корня (всех предков узла) | нет, рекурсия |
| Быстрое определение количества всех потомков узла | нет, рекурсия |
| Быстрое определение уровня | нет, рекурсия |
| Порядок следования узлов при сортировке | нет |
| Быстрая вставка новых узлов | да |
| Быстрое перемещение поддерева | да |
| Быстрое удаление поддерева | да, каскадное |
| Избыточность хранения | нет |
| Количество уровней дерева | неограничено |
| Дополнительная поддержка целостности (кроме ссылочной) | не нужна |
Подмножества
Сразу оговорюсь, к способу, продвигаемому Джо Селко (Joe Celko) и по недоразумению называемому nested sets (вложенные множества), эта схема отношения не имеет. Поэтому, чтобы избежать путаницы, я даже изменил информативное название "вложенные множества" на более простое.
В этой схеме дерево представляется вложенными подмножествами, корневой уровень включает в себя все подмножества - узлы первого уровня, те, в свою очередь, узлы второго уровня и т.д. На рисунке иерархия территорий может выглядеть так.
Рис.2. Представление иерархии в виде вложенных подмножеств
В реляционном же виде схема будет выглядеть так.
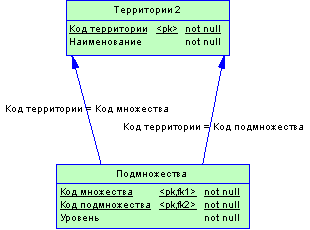
Рис.3. Реализация метода подмножеств
Целостность поддерживается триггерами, которые перезаписывают список и уровни предков данного узла при его изменении. Для удаления достаточно декларативной ссылочной целостности (каскадное).
Пример заполнения таблиц
Территории
| Код территории | Наименование |
|---|---|
| 1 | Санкт-Петербург |
| 2 | Московский район |
| 3 | МО Новоизмайловское |
Подмножества
| Код множества | Код подмножества | Уровень |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 1 | 1 |
| 3 | 2 | 2 |
| 3 | 3 | 3 |
Но за излишества надо платить. Целостность данных будет поддерживаться триггерами, которые перезаписывают список и уровни предков данного узла при его изменении. Для операции удаления достаточно декларативной ссылочной целостности (каскадное удаление), если ваша СУБД его поддерживает.
Если за образец принять список смежности, который не содержит никакой избыточности, то для метода подмножеств на каждый уровень потребуется столько дополнительных записей в таблице подмножеств, сколько элементов находится на данном уровне дерева, умноженном на номер уровня (вершину считаем первым уровнем). Количество записей растет в арифметической прогрессии.
Однако стоит взглянуть на примеры все тех же типовых запросов, как становятся очевидными преимущества, полученные от избыточности хранения: запросы стали короткими и быстрыми.
Выборка поддерева по заданному узлу:
SELECT "Код подмножества", Уровень
FROM Подмножества
WHERE "Код множества" = 123 -- корень поддерева
ORDER BY Уровень
Выборка всех предков (путь к узлу от корня):
SELECT "Код множества", Уровень
FROM Подмножества
WHERE "Код подмножества" = 345 -- узел
ORDER BY Уровень
Проверка, входит ли узел в поддерево:
SELECT result = CASE
WHEN EXISTS (
SELECT 1
FROM Подмножества
WHERE "Код подмножества" = 345 /* узел */
AND "Код множества" = 211 /* корень поддерева */
)
THEN 'Узел входит в поддерево'
ELSE 'Узел НЕ входит в поддерево'
END
Преимущества и недостатки
| Простота структуры (таблиц/ссылок/минимальное количество полей) | 2/2/5 |
|---|---|
| Прямая выборка всех детей узла | да |
| Прямая выборка поддерева (всех потомков узла) | да |
| Прямая выборка пути от узла до корня (всех предков узла) | да |
| Быстрое определение количества всех потомков узла | да |
| Быстрое определение уровня | да |
| Порядок следования узлов при сортировке | нет |
| Быстрая вставка новых узлов | нет |
| Быстрое перемещение поддерева | нет |
| Быстрое удаление поддерева | да, каскадное |
| Избыточность хранения | да |
| Количество уровней дерева | неограничено |
| Дополнительная поддержка целостности (кроме ссылочной) | нужна, простая |
Маршрут обхода
Как известно из уже упомянутой теории графов, для обхода дерева существует три способа: можно проходить узлы в префиксном, инфиксном или суффиксном порядке. Префиксный порядок обхода дерева рекурсивно определяется так: сначала корень дерева, потом узлы левого поддерева в префиксном порядке, наконец, узлы правого поддерева в префиксном порядке. Сложно? Взгляните на рис. 4, и все станет предельно ясно.
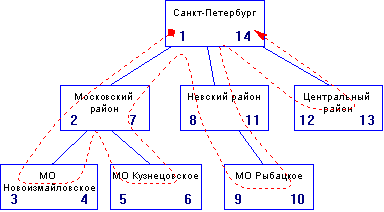
Рис.4. Маршрут обхода дерева в префиксном порядке
Хранение маршрута обхода дерева в префиксном порядке и есть тот самый способ, который его уважаемый автор Джо Селко (или его интерпретаторы), видимо, по недоразумению продвигает под названием «вложенные множества» (nested sets). По недоразумению, потому что из рис. 4 ясно, что о множествах здесь речи не идет. Однако эта неувязка с названиями нисколько не уменьшает практической ценности метода.
Квадратик на рисунке обозначает узел, цифра в левом его углу является порядковым номером этапа маршрута при входе в узел, а цифра справа — при выходе, т.е. когда тем же способом пройдены все потомки. Как нетрудно заметить, номера потомков всегда располагаются в интервале между соответствующими номерами предка, сколь угодно дальнего. Храня порядок обхода дерева (рис. 5), этим замечательным свойством можно воспользоваться в типовых запросах, избежав рекурсии.

Рис.5. Реализация хранения маршрута обхода
Очевидная сложность — пересчет порядка обхода при добавлении новых или перемещении имеющихся узлов (удаление можно игнорировать). В триггере придется реализовать последовательный порядок обхода с оптимизацией. Но, например, если добавляется элемент самого нижнего уровня, то все равно придется пересчитать все, что «выше» или «правее», а это может быть сравнимо с пересчетом маршрута по всему дереву.
Выборка поддерева по заданному узлу:
SELECT T1.*
FROM "Территории 3" AS T1, "Территории 3" AS T2
WHERE T1.Вход BETWEEN T2.Вход
AND T2.Выход
AND T2."Код территории" = 123 -- корень поддерева
ORDER BY T1.Вход
Выборка всех предков (симметрия с предыдущим запросом относительно BETWEEN):
SELECT T1.*
FROM "Территории 3" as T1, "Территории 3" as T2
WHERE T2.Вход BETWEEN T1.Вход AND T1.Выход
AND T2."Код территории" = 345 -- узел
ORDER BY T1.Вход
Проверка, входит ли узел в поддерево:
SELECT result = CASE
WHEN EXISTS (
SELECT 1
FROM "Территории 3" AS T1, "Территории 3" AS T2
WHERE T1."Код территории" = 456 /* узел */
AND T2."Код территории" = 123 /* корень поддерева */
AND T1.Вход BETWEEN T2.Вход
AND T2.Выход
)
THEN 'Узел входит в поддерево'
ELSE 'Узел НЕ входит в поддерево'
END
Преимущества и недостатки
| Простота структуры (таблиц/ссылок/минимальное количество полей) | 1/0/4 |
|---|---|
| Прямая выборка всех детей узла | да |
| Прямая выборка поддерева (всех потомков узла) | да |
| Прямая выборка пути от узла до корня (всех предков узла) | да |
| Быстрое определение количества всех потомков узла | да |
| Быстрое определение уровня | да |
| Порядок следования узлов при сортировке | да |
| Быстрая вставка новых узлов | нет |
| Быстрое перемещение поддерева | нет |
| Быстрое удаление поддерева | да |
| Избыточность хранения | да |
| Количество уровней дерева | неограничено |
| Дополнительная поддержка целостности (кроме ссылочной) | нужна, сложная |
Оптимизация: хранение номеров с "дырками"
Давным-давно в эпоху распространенности языка Бейсик (Basic, не путать с Visual Basic) строки программы последовательно нумеровались. Чтобы, во-первых, интерпретатору было легче обрабатывать текст программы, а, во-вторых, чтобы работали многочисленные операторы безусловного перехода GOTO на строку с таким-то номером, причем оператор соответствовал строке. Программа во время своей жизни модифицировалась, в нее добавлялись новые операторы. Поэтому опытные программисты нумеровали строки не 1,2,3..., а 10, 20, 30. Это позволяло вставить новую строку без полной перенумерации всех последующих.
Думаю, принцип вы уже поняли: нумеровать входы и выходы из узлов с некоторым интервалом, например 100 или 1000, что в значительной степени зависит от предварительных оценок количества хранимых строк.
Материализованные пути
Идея метода заключается в хранении пути от вершины до данного узла в явном виде и в качестве ключа. Например, иерархия территорий на рис.4 могла бы выглядеть так:
Территории
| Наименование | Путь |
|---|---|
| Санкт-Петербург | 1 |
| Московский район | 1.1 |
| МО Новоизмайловское | 1.1.1 |
| МО Кузнецовское | 1.1.2 |
| Невский район | 1.2 |
| МО Рыбацкое | 1.2.1 |
| Центральный район | 1.3 |
Данный метод является наиболее наглядным с точки зрения кодификации элементов: каждый узел получает интуитивно понятное значение, сам код и его части несут смысловую нагрузку. Подобные свойства важны в классификациях, предназначенных для широкого использования, например в стандартизованных справочниках территорий (ОКАТО), отраслей экономики (ОКВЭД, NAICS), медицинских диагнозов (МКБ — международный классификатор болезней) и во многих других областях.

Рис.6. Реализация хранения материализованных путей
Сложнее ситуация с запросами. Они лаконичны, но не всегда эффективны, так как могут требовать поиска по подстроке.
Выборка поддерева по заданному узлу:
SELECT *
FROM "Территории 4"
WHERE Путь LIKE '1.2%' -- корень поддерева
ORDER BY Путь
Выборка всех предков:
SELECT *
FROM "Территории 4"
WHERE '1.2.1' /* узел */ LIKE Путь + '%'
ORDER BY Путь
или
SELECT T1.*
FROM "Территории 4" T1, "Территории 4" T2
WHERE T2.Путь LIKE T1.Путь + '%'
AND T2.Наименование like 'МО Рыбацкое'
Проверка, входит ли узел в поддерево:
SELECT result = CASE
WHEN EXISTS (
SELECT 1
FROM "Территории 4" AS T1, "Территории 4" AS T2
WHERE T1.Наименование = 'МО Рыбацкое' /* узел */
AND T2.Наименование = 'Невский район' /* корень поддерева */
AND T1.Путь LIKE T2.Путь + '%'
)
THEN 'Узел входит в поддерево'
ELSE 'Узел НЕ входит в поддерево'
END
Оптимизация
Зная заранее максимальное количество уровней и максимально число прямых потомков, можно обойтись без разделителей, используя числовые коды с фиксированной разбивкой на группы разрядов. Пустые разряды заполняются нулями. Подобная система используется во многих межсистемных классификаторах, например, относящихся к государственному стандарту ОКАТО (Общероссийский классификатор объектов административно-территориального деления) или NAICS (North American Industry Classification System - Североамериканская система классификации отраслей экономики).
Преимущества и недостатки
| Простота структуры (таблиц/ссылок/минимальное количество полей) | 1/0/2 |
|---|---|
| Прямая выборка всех детей узла | да |
| Прямая выборка поддерева (всех потомков узла) | да |
| Прямая выборка пути от узла до корня (всех предков узла) | да |
| Быстрое определение количества всех потомков узла | да |
| Быстрое определение уровня | да |
| Порядок следования узлов при сортировке | да |
| Быстрая вставка новых узлов | нет |
| Быстрое перемещение поддерева | нет |
| Быстрое удаление поддерева | нет |
| Избыточность хранения | да |
| Количество уровней дерева | ограничено |
| Дополнительная поддержка целостности (кроме ссылочной) | нужна, сложная |
Итоги
| Списки смежности | Подмножества | Хранение маршрута обхода | Материализованные пути | |
|---|---|---|---|---|
| Простота структуры (таблиц/ссылок/минимальное количество полей) | 1/1/3 | 2/2/5 | 1/0/4 | 1/0/2 |
| Прямая выборка всех детей узла | да | да | да | да |
| Прямая выборка поддерева (всех потомков узла) | нет, рекурсия | да | да | да |
| Прямая выборка пути от узла до корня (всех предков узла) | нет, рекурсия | да | да | да |
| Быстрое определение количества всех потомков узла | нет, рекурсия | да | да | да |
| Быстрое определение уровня | нет, рекурсия | да | да | да |
| Порядок следования узлов при сортировке | нет | нет | да | да |
| Быстрая вставка новых узлов | да | нет | нет | нет |
| Быстрое перемещение поддерева | да | нет | нет | нет |
| Быстрое удаление поддерева | да, каскадное | да, каскадное | да | нет |
| Избыточность хранения | нет | да | да | да |
| Количество уровней дерева | неограниченное | неограниченное | неограниченное | ограниченное |
| Дополнительная поддержка целостности (кроме ссылочной) | не нужна | нужна | нужна | нужна |
Источники
- Joe Celko. Trees in SQL. Some answers to some common questions about SQL trees and hierarchies
- Vadim Tropashko. Trees in SQL: Nested Sets and Materialized Path
- Джо Селко. Стиль программирования Джо Селко на SQL. Пер. с англ. СПб.: Питер, 2006.
Сергей Тарасов, октябрь 2006